0. 방문해주신 분들께
생각보다 글을 쓰는게 조금 늦어졌네요. 아무래도 학기중에 밀린 업무들을 처리하느라 일을 풀타임으로 뛰다 보니 몇 주가 순식간에 지나간 것 같습니다.
아마 이게 지금까지 시리즈로 작성해오던 회고록의 마지막 글이 될 것 같네요. 재미있게 읽어주시면 감사하겠습니다!
(2025.03.12 추가)
계속 미루고 미루다가 결국 한 학기가 지난 후에야 글을 마무리하게 되었습니다. 죄송합니다(…) 한 학기동안 많은 분들이 이 블로그의 TUM관련 글들을 통해 연락을 주셨습니다. 책임감을 느끼고 이제라도 시리즈를 마무리하려고 합니다 :)
핑계일 수 있지만 글을 빠르게 적지 못한 이유는 제가 THEO라는 과목의 전문가가 아닌 것에 있습니다. 그만큼 어려운 과목이었고 수월히 통과한 지금도 제가 저 과목을 완벽히 이해했나? 라고 스스로 묻는다면 시원하게 YES라고 대답을 할 수가 없네요.
어디까지나 학부생의 입장에서 쓴 글이므로 내용이 정확하지 않을 수 있습니다. 꼭 참고해주세요.
1. 글을 시작하며
1학년 1학기부터 2학년 2학기까지, 짧다면 짧고 길다면 긴 후기글이 끝이 났다. 글을 예상보다 늦게 작성하게 된 이유는, 시험이 끝난지 얼마 되지 않은 상태에서 후기글을 즉시 작성하기에는 객관적으로 정보를 전달하기 어려울 것 같다는 판단 아래에서였다.
실제로 글을 쓰다보니 정보 전달의 성격보다는 그저 이 시험이 얼마나 어려운지를 강조하는, 일종의 겁주기에 불과한 글이 써져서 키보드에서 손을 떼고 몇 주 정도의 시간을 가졌다.
이 전 글들에서도 충분히 강조했다고 생각하지만, THEO는 그정도로 내게 트라우마를 심어줄 만큼 스스로가 스트레스를 받아가며 공부한 과목이고, 아마 내가 대학내내 가장 열심히 공부했던 과목이기도 하다.
괴짜가 아닌 평균적인 시선으로 봤을 때, THEO는 재미있다. 내 친구들을 포함해 “강의”가 재미없다고 하는 사람은 많이 보지 못했다. 정말 흥미로운 주제들로 가득한 강의의고, 강의하시는 교수님도 엄청난 열정을 가지고 학생들을 가르치신다. (Prof. Esparza) 정말 “강의”만 듣는다면, 목차부터 실제 Tutorium 세션까지 - 이렇게 잘 구성된 강의를 TUM에서 본 적이 있었나 싶을 정도로 괜찮은 강의었다. 하지만:
교수님이 이 과목에서 많은 학생들이 떨어지는 것에 자부심을 가지고 계신다(…)
이로 인해 시험이 정말 어렵게 출제되고, 또 많은 학생들을 좌절케하는 과목이 되어버렸다.
짧게 줄이고, Theoretische Informatik, 학사 전에 넘어야 할 사실상의 최종관문. 1학년때부터 숱하게 악명을 들어왔으며, 실제로 그 악명의 값을 톡톡히 해냈던- 그만큼 통과했을때의 성취감과 기쁨도 컸던 애증의 과목에 대해 자세히 알아보자.
2. Theoretische Informatik, 뭘 하는 과목일까?
Theoretische Informatik(이하 THEO)는 이론전산학으로서, 크게 두 가지 부문에 대해 공부한다:
- Formal Language (형식 언어)
- Computability, Computable Set (계산 가능성 이론)
조금 더 High Level에서 설명하자면
- 컴퓨터가 어떻게 인간의 언어인 알파벳을 “이해”(decompile)할 수 있는지,
- 컴퓨터가 계산할 수 있는 문제의 범위는 어디까지인지 / 계산할 수 없는 문제가 있다면, 어째서 그러한지
이 정도로 간략하게 표현할 수 있겠다. 이렇게 들으면 굉장히 추상적인 과목으로 들리지만, 사실 그렇게까지 뜬구름잡는 성격의 강의는 아니다. 하지만 감이 오듯이 많은 부분에서 증명이 바탕이 되며, 증명을 제대로 이해하지 못할 시 강의나 문제풀이에 많은 어려움이 있다. 각각의 부분에 대해 조금 더 자세히 알아보는 시간을 갖자.
2.1 Formal Language
Formal Language 파트에선 대부분 컴퓨터 과학에서 말하는 “문법”과 이를 decompile 할 수 있는, 즉, 어떠한 단어가 주어졌을 때 그 단어가 문법에 맞는지를 판별해내는 오토마타에 관해 심도있게 공부한다. (가끔 추상적으로 표현된 언어를 우리가 정규식으로 바꾼 후 문제에 접근해야 하는 경우도 존재한다.)
이렇게 말하면 감을 잡기 어려우니 아주 간단한 예시를 들어보자.
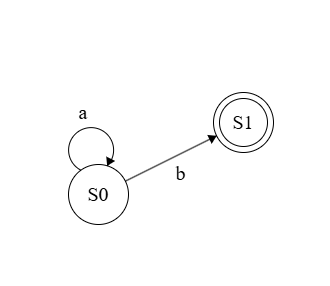
문법 L = a*b 가 주어졌다고 가정해보겠다. 여기서 별표는 a가 유한하게 반복될 수 있음을 의미한다. 즉. L이라는 문법의 언어는:
G(L) = {b, ab, aab, aaab …} 로 표현할 수 있다.
그렇다면 어떠한 단어가 이 언어 G에 포함되는지를 완벽히 판별해 낼 수 있는 오토마타가 존재할까? 정답은 YES이다. (이 또한 강의에서 증명한다.)
위의 그림이 이 언어를 완벽히 표현하는 오토마타이다. 표면적으로는 이런 것들을 한 학기 내내 배우게 된다.
이 예시는 아주 간단한 예시이고, 당연히 수업에는 온갖 복잡한 문법과 언어들이 등장한다. 그리고 당연히 문법들이 복잡해질수록 오토마타 또한 굉장히 그리기 어려워지는데, 이런 부분들이 시험에 꼭 나온다.
가장 간단한 Rechtslineare Grammatik(정규 표현식)으로부터 시작해 Kontextfreie Grammatik, Phrasenstrukturgrammatik등을 배우는데, Rechtslineare Grammatik까지야 정규 표현식이고 실제로 코딩할때도 많이 쓰는 부분이라 어찌저찌 이해한다고 쳐도 Kontextfreie Grammatik부터는 일반적인 오토마타로는 표현할 수 없어 Kellerautomat등의 굉장히 특이하고, 시험 문제에서 실제로 풀기 위해서는 직관(운 또는 재능?)이 필요한 도구들이 나온다. 깊게 설명하기에는 너무 깊은 내용들이니 직관적으로 표현하고 파트 2.1을 마무리하도록 하겠다.
Rechtslineare Grammatik은 모든 문법에 한해 S -> aS의 형식으로 나타낼 수 있는 문법들을 말한다. 여기서 소문자는 알파벳, 그러니까 덧붙여지는 문자이고, S는 이미 그 자체로 한 단어(symbol)라고 할 수 있다. Symbol이 존재한다면 아직 Rechtslineare Grammatik에서는 모든 규칙이 Expression -> alphabet … alphabet || Expression의 형식이다. 상기의 문법 L = a*b를 문법으로 표현한다면:
S -> aS | aB
B -> b가 되는데, S -> aS를 무한히 반복하며 a의 갯수를 늘려나가다가 aB를 선택한 순간 B -> b의 문법이 활용되어 마지막 b가 붙으며 (추가적인 대문자가 없으니) 문법의 활용이 종료되어 최종적인 단어가 만들어지는 형식이다. 이러한 문법은 간편하며, 무조건 symbol(대문자)이 알파벳의 가장 오른쪽에 위치한다. 이러한 특징은 큰 장점을 지니는데, 전에 내가 어떤 문법을 선택했는지 따위의 statement를 기억할 필요가 없다. 항상 정확한 방향으로만 (오른쪽) 단어가 커지기에 단순한 직선의 벡터를 가자며, 따라서 아까 본 오토마타처럼 statement와 화살표만으로 표현되는 컴파일러(DFA or NFA)로 간단하게 표현할 수 있다.
하지만 Symbol(대문자, 전 iteration을 통해 생성된 단어 파편)이 항상 문법 가장 오른쪽에 위치해야할까? 아니다. Kontextfreie Grammaitk에서는 Symbol이 어디에도 올 수 있다. 예시를 들어보자.
S -> aSb | bSa | K
K -> empty(epsilon)이런 형식을 가지는것이 가능해진다. 이런 문법들의 문제점은 S 앞과 뒤에 뭐가 있었는지 기억해야한다는 점이다. 저 문법은 참고로 a와 b의 개수가 같은 모든 단어를 표현하는 문법이다. 그렇다면 내가 현재 가지고 있는 a의 개수가 얼마인지 아까 본 오토마타로 표현할 수 있을까? 당연히 없다.
단순히 한 방향으로 이동하기에 이 전에 a가 몇개나 쌓여있었는지 기억하는 기능은 존재하지 않는다. (다시 말하지만, 이 점도 수업시간에 증명한다.) 이런 언어를 표현하기 위해서는 간단하게나마 현재의 상태를 기억할 수 있는 컴파일러가 필요하고, 이게 Kellerautomat (혹은 stack automata)다. Kellerautomat은 statement 외에 스택 자료구조를 추가로 가지며, 이를 이용하여 전 조건으로 인한 현재 단어의 상태를 기억할 수 있다.
어렵게 느껴진다면 정상이다. 시험문제에서는 보통 괴랄한 문법을 하나 던져주고 이를 1대1대응시키는 오토마타타를 찾아라라는 식의 문제가 꼭 나오기 때문에 충분히 많은 언어들을 오토마타로 변환시키는 연습이 필요하다.
당연히 이게 끝은 아니고, 더 복잡한 문법 (Typ0 Grammatik)들도 배우는데, 이런 문법들은 더이상 오토마타가 아닌 Turing Machine으로 표현하게 된다. 어려운 문제로는 심지어 시험에서 주어진 조건의 문제를 해결하는 튜링머신을 코딩하라는 문제도 나오기도 한다. (나때는 나왔다. 나때는…) 정말 마지막으로 언어에 관한 증명 문제 (예를 들어서 언어 A가 언어 B를 포함하는가)도 많이 출제되고, 또 공부한다.
언어와 오토마타에 관해서 더 이야기 할 내용은 수도 없이 많지만, 솔직히 이 블로그에 들어와 TUM에서의 공부에 맛을 보려는(혹은 팁을 얻어가려는) 독자들에게 더 자세한 설명의 의미는 없을 것 같다. 어차피 좋든 싫든 강의에서 마주쳐 싸워나가야하는 부분이니 벌써부터 여기에 모든 Folien 내용을 다 담는다는것은 어불성설이다. 다만 공부법에 대해서는 공부법과 시험 파트에서 간단히 이야기해보도록 하겠다.
2.2 Computability, Computable Set, P/NP
P, NP와 사랑에 빠져야 하는 파트이다. 학기 마지막즈음에 공부하게 되며, 비율로 따지면 Formal Language가 70%정도, 이 파트가 30%정도를 담당한다고 할 수 있다.
여기서 배우는 것은 첫째로 Computability, 즉, 어떠한 문제를 해결하는것이 가능한가에 관한 판별법이다.
이론적으로는 어떠한 문제가 해결 가능하다면, 그 문제를 해결할 수 있는 Turing Machine이 존재해야만 한다. 즉, 알고리즘이 있어야만 한다. 이게 없다면, 그 문제는 해결이 불가능하다.
더 나아가서, 모든 언어 L에 한해서 특정 단어 w가 L에 포함되는지를(즉 컴파일) 나타내는 오토마타(2.1에서 공부한)가 존재할까? 정답은 NO이다. 특정 언어는 이론상 어떠한 오토마타로도, 어떠한 튜링 머신으로도 컴파일이 불가능하다. 이런 언어를 Unentscheidbare Sprache, non-computable language라고 한다.
이런 추상적인 개념/이를 해결하는 가상의 튜링머신의 존재유무따위를 공부하게 된다. 시험 문제는 어떤 식으로 나올까? 예시로 문제 하나를 보자.
문제) M이 어떠한 가상의 튜링머신이라고 하고, 어떠한 단어 w가 존재한다고 하자. 이 단어의 판별을 위해 튜링머신 M을 사용할때, 튜링머신 M은 멈추지 않고(final state에 도달하지 않고) 무한히 동작한다. 이 튜링 머신 M이 표현하는 언어 L(M)의 Computability에 관해 무엇을 말할 수 있는가?
문제는 대부분 이런 식이다. 어렵고, 추상적이다. 솔직히 운이 어느정도 따라줘야 맞출 수 있지만 감이 생기면 대충이나마 educated guess를 할 수 있다.
마지막 파트는 P/NP인데, 여러가지 P/NP문제에 관해 배우고 증명한 후, 우리가 알고있는 P/NP문제를 활용하여 새로운 임의의 문제의 P/NP성을 증명하는 과제가 주로 나온다.
예를 들어, P문제라고 증명된 문제들은 2COL, 2KNF-SAT가 있고, NP문제는 3COL, SAT, CLIQUE등이 있다.
새로운 임의의 문제가 주어졌을때, 이 문제를 2COL, 2KNF-SAT등으로 표현할 수 있으면, 즉 새로운 문제를 우리가 이미 알고있는 P문제로 코딩할 수 있으면 이는 P문제이다. 당연히 반대로 NP문제로 코딩할 수 있다면 이는 NP문제이다. 이 과정을 Reduktion이라고 한다.
정말 어려운 개념이지만 쉽게 말해서 2COL이라는 문제를 하나의 프로그래밍 언어라고 생각하고 이 2COL을 이용해 새로운 문제를 코딩하여 표현할 수 있는지, 이것이 Reduktion의 본질이라고 할 수 있겠다.
보통 많은 학생들은 이 파트는 포기하는 경우가 많지만(학기말이고 시험기간에 배우는 부분이라 그냥 다른 파트 공부를 더 하는 친구들이 많다) 생각보다 적응하면 쉽게 풀 수 있기 때문에 (그리고 THEO에서 흔치 않게 부분점수를 주기 때문에) 조금 공부해서 몇 점이라도 벌어가는게 좋다고 생각한다. 이 파트에 관한 공부법도 바로 밑에서 알아보자.
3. 공부법/시험
다 좋다. 그럼 도대체 이 시험을 어떻게 통과하라는 것일까? 처음엔 양에 압도될 것이고, 주위에서 듣는 괴담에 긴장하게 될 것이다. 그리고 공부를 하며 스스로 끊임없이 질문을 하게 될 수도 있다.
딱히 컴퓨터 과학에 재능이 없는 내가 이런 시험을 통과할 수 있을까?
통과할 수 있다. 그리고 그 방법은 정말 단순하다.
연습만이 살길이다.
나는 보통 4학기에 이수하는 Praktikum을 과감하게 5학기로 미루고 THEO와 DWT등의 필수과목들을 통과하는데 집중했다. 물론 이렇게까지 할 필요는 없지만 그만큼 많은 시간을 투자한다면 2학년 2학기, 지금까지 충분히 잘 해온 여러분들은 충분히 통과할 자격을 갖췄다.
평소에 예습/복습은 당연히 하는게 좋고, 시험기간은 넉넉히 두 달 정도로 잡자.
THEO시험은 강의가 끝나는 바로 그주(!) 토요일 아침 8시에 치는것이 전통이다. 따라서 조금만 긴장을 늦추면 이미 시험이 코앞까지 와있어 옴짝달싹 할 수 없는 상황이 된다. 학기 중, 6월 초에 공부를 시작하자. 또한 내가 공부한 방법은 다음과 같다.
- 모든 Übungsblätter 7회 주파 (6월 말까지)
- 모든 Altklausuren 5회 주파 (7월 중순까지)
- 시험 전날까지 Altklausuren, Übungsblätter를 비교하며 혼합하여 2회독
무식하다. 알고있다. 하지만 최고의 방법이었고, 우리 스터디에서 모두가 사용한 방법이다.
그리고 나를 포함한 스터디원 전원이 THEO 과목을 통과했다. 이는 자랑스럽게도 내가 아는 다른 스터디들 중에서도 독보적인 결과였다. 그리고 이 글을 읽는 여러분들에게도 통할 것이라고 확신한다.
반복, 반복 그리고 또 반복이 THEO 공부의 핵심이다. THEO시험이 엄청나게 창의적으로 나올것이라는 착각을 하는 친구들이 많은데, 교수진도 사람이라 늘 비슷한 패턴으로 문제가 나오고, 창의적인 문제가 나와봤자 결국 옛날에 어디서 푼 내용들을 사용하여 풀 수 있게 구성되어있다. 그런데 이런 것을 알아보려면 문제들을 보기만해도 질릴정도로, 달달 외울정도로 익숙해질 필요가 있다. 따라서 푼 문제를 지루하더라도 또 풀고, 또 정리하고, 또 분석하는 부분이 굉장히 중요하다. 학기말쯤에는 문제를 보기만해도 머리에서 답변이 그려질정도로 외웠던 것 같다.
Formal Language 파트는 이정도면 무난하게 전부 풀 수 있다. 물론 THEO의 악명은 절대 부분점수를 주지 않는 것에 있기에 실수하지않도록 조심 또 조심해야한다. 하지만 이 또한 반복훈련으로 충분히 숙달될 수 있는 부분이다.
두 번째 파트 또한 Computability까지는 문제가 늘 비슷하게 나오기 때문에 공부하며 질문들의 특징을 공부하다보면 적어도 50%정도는 무난히 맞출 수 있다. 나머지 50%는 이론 공부와 감이다.
하지만 P/NP Reduktion은 조금의 훈련이 필요한데, 솔직히 학기말에 이런 훈련을 할 시간이 너무 부족하다. THEO 시험이 너무 코앞에 위치해 있는 탓이다.
Computability와 P/NP를 공부하기 위해서는 과감히 아래의 유튜브 플레이리스트를 추천한다. 나와 내 친구들도 저 동영상을 돌려보며 공부했고, 내가 아는 한 가장 정리가 잘 되어있고 시험에서도 그대로 응용할 수 있는 테크닉들을 잘 알려주는 영상들이다.
https://www.youtube.com/watch?v=E42XIfOHnWs&list=PLG_1tsKrsKVOmNXayMalnfBJaQE5lVBis
반복, 또 반복은 시간 싸움이다. 다시한번 강조하지만, 최대한 일찍 시작하자. 놀랍게도 시간을 때려부으면 THEO를 통과할 수 있다는건 나를 통해, 내 스터디원들을 통해 증명된 내용이다. (몇 명을 제외하고는 다들 빈말로라도 천재라고 할 수 없는 친구들이다.)
의심하지 말고 달리자. 내 경험상 스스로에 관한 의심이 THEO를 어렵게 만든 가장 큰 범인이었다.
5. 후기
여기까지 무사히 마치셨다면, 축하합니다! :) 여러분은 이제 TUM을 성공적으로 졸업할 수 있는 모든 요건을 갖추시게 되었네요.
제가 이 글을 마무리하는 시점인 5학기 말을 돌아보면, 남은 1년은 정말 대학생활을 즐기시면서 천천히 진로에 대해 탐색하며 스펙을 쌓는 시간으로 삼아도 좋을 만큼 시간/심적 여유가 넉넉해진다고 자신있게 말씀드릴 수 있을 것 같습니다.
물론 펑펑 놀기만 하는게 좋은 건 아니겠죠? 여러가지 자격증을 준비한다던지, Werkstudent나 Praktikum을 한다던지 등의 계획을 잘 세워서 알찬 학사의 마무리를 보내시기를 바라겠습니다.
이번 시리즈를 쓰면서 TUM에서의 공부에 대한 이야기는 대부분 마친 것 같습니다. 이 외에 유학생활이나 타향살이에 대한 제 생각은 천천히 정리하여 추후 번외편으로 찾아뵙겠습니다, 감사합니다. 글 읽느라, 공부하느라 고생하셨어요!
Aller Anfang ist schwer. Nicht nur für dich.